19 グラフ,ネットワーク,木
Contents
- 「グラフ」数学で使われる場合のグラフのことで,ノード(node) や節(vertex)と呼ばれる点と,それをつなぐ,弧(arc)や辺 (edge)と呼ばれるものから構成されている. グラフの中には,ネットワークや木なども含まれている. グラフとネットワークについては,続く節で解説する. 木については,19.2 木 と19.3 他の木表現で解説 する. 74
- 「チャート」複数の軸(次元)を持つ図上でデータを表現するもの で,直交軸や放射軸上のグラフや,棒グラフ,円グラフなどがあ る(訳注:チャートとは,日本の高校までの数学で使われる「グ ラフ」に相当するもの.). これらは,図や表向けのモジュールで規定されている要素で表現 することができる. 詳細は,14 図・表・式を参照のこと.
グラフで表現されるものには,例えば,組織の階層,フローチャー ト,系譜,意味ネットワーク,遷移ネットワーク,文法関係,トーナ メント表,座席表,道順などがある. このような各種の対象をグラフで表現するガイドラインを示すにあた り,数学による形式的な定義と,もっとも一般的な表現法を使うこと にする. 但し,本章で推奨するものは,グラフを使って表現できる全ての対象 を網羅しているものではないことは強調しておく必要がある. 本章では,デザイン,レイアウト,配置などで特に問題となるものの みを扱っている.
19.1 有向グラフ・無向グラフTEI: 有向グラフ・無向グラフ¶
ここで,少し用語の解説をしておく. グラフにおける「パス」とは,ノード列のことで,i番目のノード とi+1番目のノード間にある弧(辺)の連接から構成されるものである. 「巡回パス」または「閉路」とは,あるノードから始まるパスが, そのノードにまた戻るものである. 少なくとも1つの閉路を持つグラフは「巡回している(cyclic)」といい,そ うでないものを「巡回していない(acyclic)」という. 最後にもうひとつ,グラフが「連結」しているとは,あるノードか ら他の全てのノードへのパスが存在している時のことをいう. 連結していないグラフは,「非連結」という.
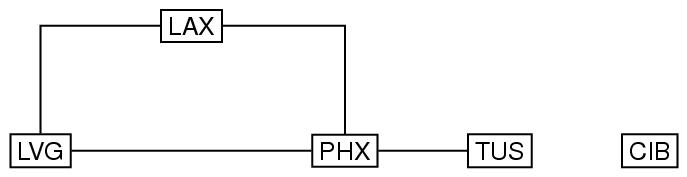
無向グラフで,非連結の巡回グラフの例をみてみよう. ここでは,3文字の名前で示された各ノードは,空港を表現したも ので,ノードをつなぐ各弧は,垂直の線と水平の線で示されている. 各線が90度で曲がっているのは,単に,斜線を使いたくなかった為 である.
type="undirected"
xml:id="CUG1"
order="5"
size="4">
<label>Airline Connections in Southwestern USA</label>
<node xml:id="LAX" degree="2">
<label>LAX</label>
</node>
<node xml:id="LVG" degree="2">
<label>LVG</label>
</node>
<node xml:id="PHX" degree="3">
<label>PHX</label>
</node>
<node xml:id="TUS" degree="1">
<label>TUS</label>
</node>
<node xml:id="CIB" degree="0">
<label>CIB</label>
</node>
<arc from="#LAX" to="#LVG"/>
<arc from="#LAX" to="#PHX"/>
<arc from="#LVG" to="#PHX"/>
<arc from="#PHX" to="#TUS"/>
</graph>
要素graphの第一の子要素は,要素labelで, 当該グラフのラベルを記録することができる. 要素node も,当該ノードのラベルを,要素labelで記録することになる. 要素graphの属性orderとsizeは, それぞれ,ノードの数と弧(辺)の数を記録するものである. これらの属性は(グラフの情報全体から,計算して求めることもで きることから)任意であるが,その値が記録されていれば,以降の 符号化の作業で,大変便利である. また,これらの属性があれば,グラフを符号化や交換を正確に処理 する手助けとなる. 要素node の属性degreeには,ノードに接続する 弧(辺)の数を記録することになる. この属性は(冗長になるため)選択的であるが,グラフを検証する際 には有用である. もしこの属性値を付与する場合には,当該グラフ中で整合性が保た れる必要がある. 要素arcの属性from とtoは,それぞれ,弧(辺)が接続する ノードを参照するものである. この例では,無向グラフであることから,属性fromとtoを使って いながらも,それは方向性を意味していない. この2つの属性値を互いに交換しても,当該グラフには何ら影響を 与えることはない.
type="undirected"
xml:id="CUG2"
order="5"
size="4">
<label>Airline Connections in Southwestern USA</label>
<node xml:id="LAX2" degree="2" adj="#LVG2 #PHX2">
<label>LAX2</label>
</node>
<node xml:id="LVG2" degree="2" adj="#LAX2 #PHX2">
<label>LVG2</label>
</node>
<node xml:id="PHX2" degree="3" adj="#LAX2 #LVG2 #TUS2">
<label>PHX2</label>
</node>
<node xml:id="TUS2" degree="1" adj="#PHX2">
<label>TUS2</label>
</node>
<node xml:id="CIB2" degree="0">
<label>CIB2</label>
</node>
</graph>
type="undirected"
xml:id="CUG3"
order="5"
size="4">
<label>Airline Connections in Southwestern USA</label>
<node xml:id="LAX3" degree="2" adj="#LVG3 #PHX3">
<label>LAX3</label>
</node>
<node xml:id="LVG3" degree="2" adj="#PHX3">
<label>LVG3</label>
</node>
<node xml:id="PHX3" degree="3" adj="#TUS3">
<label>PHX3</label>
</node>
<node xml:id="TUS3" degree="1">
<label>TUS3</label>
</node>
<node xml:id="CIB3" degree="0">
<label>CIB3</label>
</node>
</graph>
多くの場合,要素arcを使った記述は(隣接するノードの属性 で,辺は表現することができるから)冗長なものとなるが,本モジュー ルでは,これを採用している. これにより,弧(辺)の識別子や,表示の様子,ラベルなどを(属性 xml:id,rendや,子要素labelを使い)簡単に表現することが出来る.
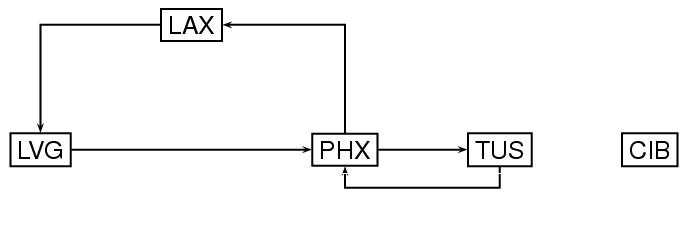
次に,先に例示したグラフを,有向グラフにしてみよう. 例えば,ある空港から別の空港までの特定ルートに,方向を付けて,以 下のようなダイアグラムを作るのである.
type="directed"
xml:id="RDG1"
order="5"
size="5">
<label>Selected Airline Routes in Southwestern USA</label>
<node xml:id="LAX4" inDegree="1" outDegree="1">
<label>LAX4</label>
</node>
<node xml:id="LVG4" inDegree="1" outDegree="1">
<label>LVG4</label>
</node>
<node xml:id="PHX4" inDegree="2" outDegree="2">
<label>PHX4</label>
</node>
<node xml:id="TUS4" inDegree="1" outDegree="1">
<label>TUS4</label>
</node>
<node xml:id="CIB4" inDegree="0" outDegree="0">
<label>CIB4</label>
</node>
<arc from="#LAX4" to="#LVG4"/>
<arc from="#LVG4" to="#PHX4"/>
<arc from="#PHX4" to="#LAX4"/>
<arc from="#PHX4" to="#TUS4"/>
<arc from="#TUS4" to="#PHX4"/>
</graph>
type="directed"
xml:id="RDG2"
order="5"
size="5">
<label>Selected Airline Routes in Southwestern USA</label>
<node
xml:id="LAX5"
inDegree="1"
outDegree="1"
adjTo="#LVG5"
adjFrom="#PHX5">
<label>LAX5</label>
</node>
<node
xml:id="LVG5"
inDegree="1"
outDegree="1"
adjFrom="#LAX5"
adjTo="#PHX5">
<label>LVG5</label>
</node>
<node
xml:id="PHX5"
inDegree="2"
outDegree="2"
adjTo="#LAX5 #TUS"
adjFrom="#LVG5 #TUS5">
<label>PHX5</label>
</node>
<node
xml:id="TUS5"
inDegree="1"
outDegree="1"
adjTo="#PHX5"
adjFrom="#PHX5">
<label>TUS5</label>
</node>
<node xml:id="CIB5" inDegree="0" outDegree="0">
<label>CIB5</label>
</node>
</graph>
type="directed"
xml:id="RDG3"
order="5"
size="5">
<label>Selected Airline Routes in Southwestern USA</label>
<node xml:id="LAX6">
<label>LAX6</label>
</node>
<node xml:id="LVG6">
<label>LVG6</label>
</node>
<node xml:id="PHX6">
<label>PHX6</label>
</node>
<node xml:id="TUS6">
<label>TUS6</label>
</node>
<node xml:id="CIB6">
<label>CIB6</label>
</node>
<arc from="#LAX6" to="#LVG6">
<label>SW117</label>
</arc>
<arc from="#LVG6" to="#PHX6">
<label>SW711</label>
</arc>
<arc from="#PHX6" to="#LAX6">
<label>AA218</label>
</arc>
<arc from="#PHX6" to="#TUS6">
<label>AW229</label>
</arc>
<arc from="#TUS6" to="#PHX6">
<label>AW225</label>
</arc>
</graph>
- » 19.1.2 系統樹
- Home | 目次
19.1.1 遷移ネットワークTEI: 遷移ネットワーク ¶
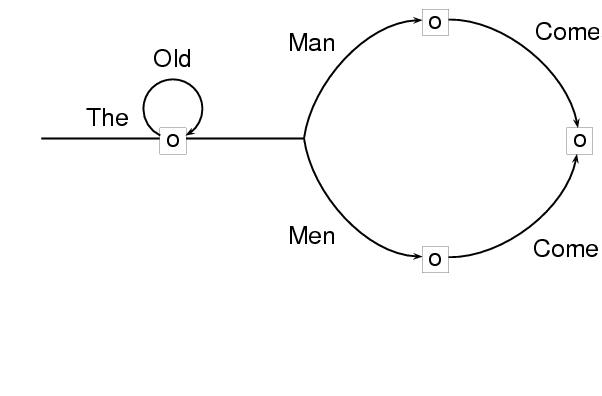
遷移ネットワークや,ノードの種類を分ける必要がある有向グラ フを符号化するには,要素nodeに属性typeを使うことになる. 以下の例では,開始ノード(または状態)と終了ノード(または状 態)は区別されている. このグラフは,開始ノードから終了ノードまでの遷移の間に,ラ ベルとして示されている一連の文字列を受理する仕組みを示して いる.
type="network-transition"
xml:id="SS8"
order="5"
size="6">
<label>(8)</label>
<node
xml:id="Q0"
inDegree="0"
outDegree="1"
type="initial"/>
<node xml:id="Q1" inDegree="2" outDegree="3"/>
<node xml:id="Q2" inDegree="1" outDegree="1"/>
<node xml:id="Q3" inDegree="1" outDegree="1"/>
<node
xml:id="Q4"
inDegree="2"
outDegree="0"
type="final"/>
<arc from="#Q0" to="#Q1">
<label>THE</label>
</arc>
<arc from="#Q1" to="#Q1">
<label>OLD</label>
</arc>
<arc from="#Q1" to="#Q2">
<label>MAN</label>
</arc>
<arc from="#Q1" to="#Q3">
<label>MEN</label>
</arc>
<arc from="#Q2" to="#Q4">
<label>COMES</label>
</arc>
<arc from="#Q3" to="#Q4">
<label>COME</label>
</arc>
</graph>
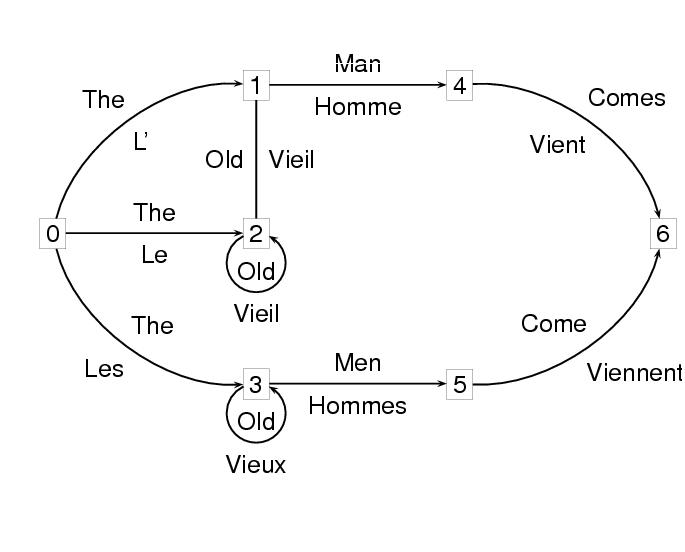
有限状態変換器では,各弧(辺)に2つのラベルがあり,この2つの ラベルは,一方から他方へ対応していることを示している. 以下の例では,英語の文字列をフランス語へと翻訳する変換器を 示したものである. 便宜上,ノードには数字を振ってある.
<node
xml:id="T0"
inDegree="0"
outDegree="3"
type="initial">
<label>0</label>
</node>
<node xml:id="T1" inDegree="2" outDegree="1">
<label>1</label>
</node>
<node xml:id="T2" inDegree="2" outDegree="2">
<label>2</label>
</node>
<node xml:id="T3" inDegree="2" outDegree="2">
<label>3</label>
</node>
<node xml:id="T4" inDegree="1" outDegree="1">
<label>4</label>
</node>
<node xml:id="T5" inDegree="1" outDegree="1">
<label>5</label>
</node>
<node
xml:id="T6"
inDegree="2"
outDegree="0"
type="final">
<label>6</label>
</node>
<arc from="#T0" to="#T1">
<label>THE</label>
<label>L'</label>
</arc>
<arc from="#T0" to="#T2">
<label>THE</label>
<label>LE</label>
</arc>
<arc from="#T0" to="#T3">
<label>THE</label>
<label>LES</label>
</arc>
<arc from="#T1" to="#T4">
<label>MAN</label>
<label>HOMME</label>
</arc>
<arc from="#T2" to="#T1">
<label>OLD</label>
<label>VIEIL</label>
</arc>
<arc from="#T2" to="#T2">
<label>OLD</label>
<label>VIEIL</label>
</arc>
<arc from="#T3" to="#T3">
<label>OLD</label>
<label>VIEUX</label>
</arc>
<arc from="#T3" to="#T5">
<label>MEN</label>
<label>HOMMES</label>
</arc>
<arc from="#T4" to="#T6">
<label>COMES</label>
<label>VIENT</label>
</arc>
<arc from="#T5" to="#T6">
<label>COME</label>
<label>VIENNENT</label>
</arc>
</graph>
- « 19.1.1 遷移ネットワーク
- » 19.1.3 歴史的解釈の表現
- Home | 目次
19.1.2 系統樹TEI: 系統樹¶
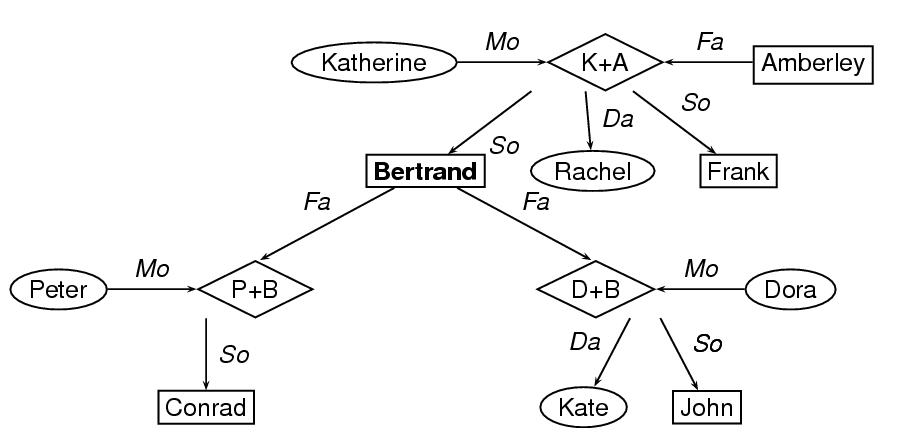
以下の例は,家系図を符号化したものである. 各ノードは,個人やその親などを示し,各弧(辺)は,親子関係や 系統関係を示している. ここでは,各個人は,素性構造を持ち,さらに素性構造ライブラ リが他で定義されているとしよう(18.4 素性ライブラリと素性値ライブラリを参照のこと). 素性構造への参照は,要素nodeで属性valueを使うことで可能となる. 以下にあるグラフでは,女性を示すノードは楕円形で示され,男性 を示すノードは方形で示され,親を示すノードは,菱形で示さ れている.
<node
xml:id="KATHR"
value="http://example.com/russell-fs/tei/kr1"
inDegree="0"
outDegree="1">
<label>Katherine</label>
</node>
<node
xml:id="AMBER"
value="http://example.com/russell-fs/tei/ar1"
inDegree="0"
outDegree="1">
<label>Amberley</label>
</node>
<node xml:id="KAR" inDegree="2" outDegree="3">
<label>K+A</label>
</node>
<node
xml:id="BERTR"
value="http://example.com/russell-fs/tei/br1"
inDegree="1"
outDegree="2">
<label>Bertrand</label>
</node>
<node
xml:id="PETER"
value="http://example.com/russell-fs/tei/pr1"
inDegree="0"
outDegree="1">
<label>Peter</label>
</node>
<node
xml:id="DORAR"
value="http://example.com/russell-fs/tei/dr1"
inDegree="0"
outDegree="1">
<label>Dora</label>
</node>
<node xml:id="PBR" inDegree="2" outDegree="1">
<label>P+B</label>
</node>
<node xml:id="DBR" inDegree="2" outDegree="2">
<label>D+B</label>
</node>
<node
xml:id="FRANR"
value="http://example.com/russell-fs/tei/fr1"
inDegree="1"
outDegree="0">
<label>Frank</label>
</node>
<node
xml:id="RACHR"
value="http://example.com/russell-fs/tei/rr1"
inDegree="1"
outDegree="0">
<label>Rachel</label>
</node>
<node
xml:id="CONRR"
value="http://example.com/russell-fs/tei/cr1"
inDegree="1"
outDegree="0">
<label>Conrad</label>
</node>
<node
xml:id="KATER"
value="http://example.com/russell-fs/tei/kr2"
inDegree="1"
outDegree="0">
<label>Kate</label>
</node>
<node
xml:id="JOHNR"
value="http://example.com/russell-fs/tei/jr1"
inDegree="1"
outDegree="0">
<label>John</label>
</node>
<arc from="#KATHR" to="#KAR">
<label>Mo</label>
</arc>
<arc from="#AMBER" to="#KAR">
<label>Fa</label>
</arc>
<arc from="#KAR" to="#BERTR">
<label>So</label>
</arc>
<arc from="#KAR" to="#FRANR">
<label>So</label>
</arc>
<arc from="#KAR" to="#RACHR">
<label>Da</label>
</arc>
<arc from="#PETER" to="#PBR">
<label>Mo</label>
</arc>
<arc from="#BERTR" to="#PBR">
<label>Fa</label>
</arc>
<arc from="#PBR" to="#CONRR">
<label>So</label>
</arc>
<arc from="#DORAR" to="#DBR">
<label>Mo</label>
</arc>
<arc from="#BERTR" to="#DBR">
<label>Fa</label>
</arc>
<arc from="#DBR" to="#KATER">
<label>Da</label>
</arc>
<arc from="#DBR" to="#JOHNR">
<label>So</label>
</arc>
</graph>
- « 19.1.2 系統樹
- Home | 目次
19.1.3 歴史的解釈の表現TEI: 歴史的解釈の表現 ¶
ヘクター・マクネイル(Hector Mcneil)は,この内容を1963年5 月28日に確認し,1632年6月15日に,エジンバラで[...].
この内容はアーガイルの前太守アーチボルト(Archibald)が保 証し,ガラハルジ(Gallachalzie)のドナルト・マクニールが前 大使から言い伝えられたことを保証するものである.
この内容は,アーガイル州にある クナプダル(Knapdale)にあるものと,それに隣接するガラハルジの2つの土地と,そ こにある付帯物について述べるものである.
(認められた他の土地についての解説が続く)
この保証書は,1669年5月15日に記された.
この例にある,ある土地とそこにある付帯物(その土地からの収入も含 む)について考えてみる.
- アーガイルの太守の土地(この保証書が保証する土地になる).
- ガラハルジにある2つの土地.
- この土地にある付帯物.
- クナプダルの所有権
- アーガイル州
- 含む(INCLUDE)
- 中にある(IN)
- 隣接する(BY)
- 一部である(PART OF)
ここで,ガラハルジ(Gallachalzie),クナプダル(Knapdale),アー ガイル(Argyll)を記録する素性構造分析を考えてみよう. これらの土地を示すノードで,属性valueを使うと,当該素性構造を関連づけること ができる. 但し,「アーガイル州の中」という句が修飾する名詞 句がどれであるのかについて不明な点は残ることになる. 恐らく,当該土地の全て(土地と付帯物)がアーガイルの中にある か,または,その付帯物のみが中にあるか,またはクナプダルだけ が(そこにある付帯物と共に)中にある,ということになるのだろう. このような3つの解釈をグラフで表現してみよう. 但し,これらは排他的な関係にあることから,16 リンク,分割,統合で解説する属性 excludeを使い,これを表現することに する. 75
実際のグラフと,その符号化したものを以下に載せる. グラフにある点線は,排他的な関係にあることを示している. 符号化テキスト中では,これは,属性excludeで記録されている.
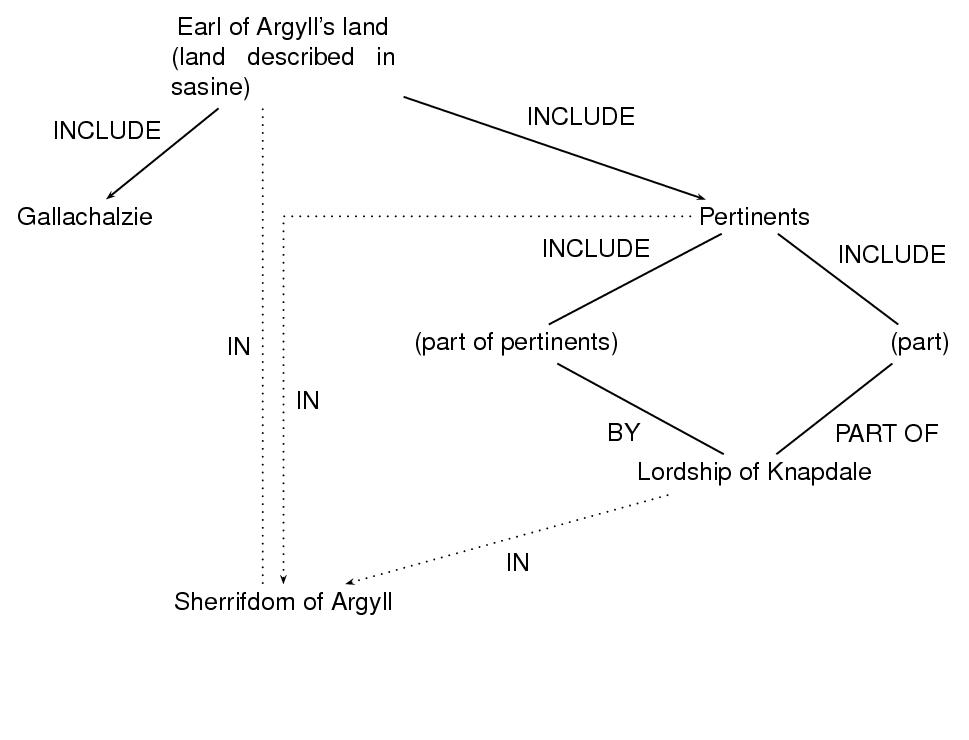 このグラフは,以下の関係を定義している.
このグラフは,以下の関係を定義している.
- アーガイルの太守の土地は,ガラハルジ(の一画)を含んでい る.
- アーガイルの太守の土地は,その一画の付帯物を含んでいる.
- その付帯物(の一部)は,クナプダルの所有地に隣接している.
- その付帯物(の一部)は,クナプダルの所有地の一部である.
- アーガイルの太守の土地,またはその付帯物,またはクナプ ダルの所有地は,アーガイル州の中にある.
<node xml:id="EARL">
<label>Earl of Argyll's land</label>
</node>
<node xml:id="GALL"
value="http://example.com/people/scots#gall">
<label>Gallachalzie</label>
</node>
<node xml:id="PERT">
<label>Pertinents</label>
</node>
<node xml:id="PER1">
<label>Pertinents part</label>
</node>
<node xml:id="PER2">
<label>Pertinents part</label>
</node>
<node
xml:id="KNAP"
value="http://example.com/people/scots#knapfs">
<label>Lordship of Knapdale</label>
</node>
<node
xml:id="ARGY"
value="http://example.com/people/scots#argyfs">
<label>Sherrifdome of Argyll</label>
</node>
<arc xml:id="EARLGALL" from="#EARL" to="#GALL">
<label>INCLUDE</label>
</arc>
<arc
xml:id="EARLARGY"
from="#EARL"
to="#ARGY"
exclude="#PERTARGY #KNAPARGY">
<label>IN</label>
</arc>
<arc xml:id="EARLPERT" from="#EARL" to="#PERT">
<label>INCLUDE</label>
</arc>
<arc xml:id="PERTPER1" from="#PERT" to="#PER1">
<label>INCLUDE</label>
</arc>
<arc xml:id="PERTPER2" from="#PERT" to="#PER2">
<label>INCLUDE</label>
</arc>
<arc
xml:id="PERTARGY"
from="#PERT"
to="#ARGY"
exclude="#EARLARGY #KNAPARGY">
<label>IN</label>
</arc>
<arc xml:id="PER1KNAP" from="#PER1" to="#KNAP">
<label>BY</label>
</arc>
<arc xml:id="PER2KNAP" from="#PER2" to="#KNAP">
<label>PART OF</label>
</arc>
<arc
xml:id="KNAPARGY"
from="#KNAP"
to="#ARGY"
exclude="#EARLARGY #PERTARGY">
<label>IN</label>
</arc>
</graph>
- « 19.1 有向グラフ・無向グラフ
- » 19.3 他の木表現
- Home | 目次
19.2 木TEI: 木¶
- tree
根,内部ノード,葉,弧(または辺)から成る木を示す.
arity 木構造における,根や内部ノードが持つ子供の最大数を示 す. ord 当該木構造が,順序付き木,または半順序付き木であるか どうかを示す. order 木構造の順番を示す.例えば,ノードの番号を示す. - root
木の根要素を示す.
value 当該根要素の値絵お示す.これは,素性構造または他の分 析要素となる. children 当該根要素の子要素となる要素の識別子のリストを示す. ord 当該根要素が,順序付きかどうかを示す. outDegree 当該根要素の出の次数,すなわち子要素の数を示す. - iNode
木における内部ノードを示す.
value 内部ノードの値を示す.素性構造向け要素または分析向け 要素になる. children 当該内部ノードの子要素の識別子をまとめたリストを示す. parent 当該ノードの親要素の識別子を示す. ord 当該内部ノードが順序付きかどうかを示す. follow 当該ノードの姉要素の識別子を示す. outDegree 内部ノードの出の次数(子要素の数)を示す. - leaf
木(構造)における葉(終端ノード)を示す.
value 素性構造または他の分析要素へのポインタを示す. parent 葉の親要素の識別子を示す. follow 当該葉の姉要素の識別子を示す.
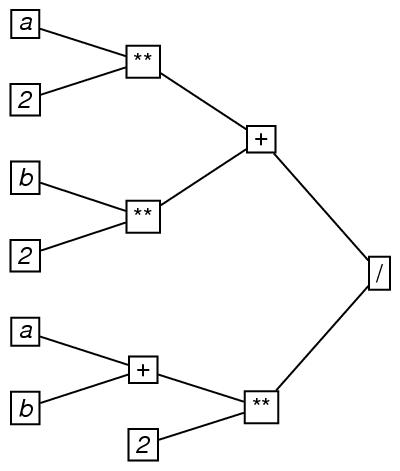
木の例を考えてみる. 以下の木では,加算(+),累乗(**),除算 (/)が,式((a**2)+(b**2))/((a+b)**2)において 働く順番を示している. このグラフでは,根要素は右側に書かれているので,木の方向は,右 から左へとされる.
n="ex1"
arity="2"
ord="true"
order="12">
<root xml:id="G-DIV1" children="#PLU1 #EXP1">
<label>/</label>
</root>
<iNode xml:id="PLU1" parent="#G-DIV1" children="#EXP2 #EXP3">
<label>+</label>
</iNode>
<iNode xml:id="EXP1" parent="#G-DIV1" children="#PLU2 #NUM2.3">
<label>**</label>
</iNode>
<iNode xml:id="EXP2" parent="#PLU1" children="#VARA1 #NUM2.1">
<label>**</label>
</iNode>
<iNode xml:id="EXP3" parent="#PLU1" children="#VARB1 #NUM2.2">
<label>**</label>
</iNode>
<iNode xml:id="PLU2" parent="#EXP1" children="#VARA2 #VARB2">
<label>+</label>
</iNode>
<leaf xml:id="VARA1" parent="#EXP2">
<label>a</label>
</leaf>
<leaf xml:id="NUM2.1" parent="#EXP2">
<label>2</label>
</leaf>
<leaf xml:id="VARB1" parent="#EXP3">
<label>b</label>
</leaf>
<leaf xml:id="NUM2.2" parent="#EXP3">
<label>2</label>
</leaf>
<leaf xml:id="VARA2" parent="#PLU2">
<label>a</label>
</leaf>
<leaf xml:id="VARB2" parent="#PLU2">
<label>b</label>
</leaf>
<leaf xml:id="NUM2.3" parent="#EXP1">
<label>2</label>
</leaf>
</tree>
この符号化テキストでは,属性arityが木 の次数(訳注:原語arityが,グラフの次数(degree)の意味で使われて いる)を示している. これは,木の中にあるノードにある属性outDegreeの属性値の最大値を示している. この例のように,属性arityの値が2であるような木は「二分木」と呼ばれる.
n="ex2"
ord="partial"
arity="2"
order="13">
<root xml:id="div1" ord="true" children="#plu1 #exp1">
<label>/</label>
</root>
<iNode
xml:id="plu1"
ord="false"
parent="#div1"
children="#exp2 #exp3">
<label>+</label>
</iNode>
<iNode
xml:id="exp1"
ord="true"
parent="#div1"
children="#plu2 #num2.3">
<label>**</label>
</iNode>
<iNode
xml:id="exp2"
ord="true"
parent="#plu1"
children="#vara1 #num2.1">
<label>**</label>
</iNode>
<iNode
xml:id="exp3"
ord="true"
parent="#plu1"
children="#varb1 #num2.2">
<label>**</label>
</iNode>
<iNode
xml:id="plu2"
ord="false"
parent="#exp1"
children="#vara2 #varb2">
<label>+</label>
</iNode>
<leaf xml:id="vara1" parent="#exp2">
<label>a</label>
</leaf>
<leaf xml:id="num2.1" parent="#exp2">
<label>2</label>
</leaf>
<leaf xml:id="varb1" parent="#exp3">
<label>b</label>
</leaf>
<leaf xml:id="num2.2" parent="#exp3">
<label>2</label>
</leaf>
<leaf xml:id="vara2" parent="#plu2">
<label>a</label>
</leaf>
<leaf xml:id="varb2" parent="#plu2">
<label>b</label>
</leaf>
<leaf xml:id="num2.3" parent="#exp1">
<label>2</label>
</leaf>
</tree>
- ((a**2)+(b**2))/((a+b)**2)
- ((b**2)+(a**2))/((a+b)**2)
- ((a**2)+(b**2))/((b+a)**2)
- ((b**2)+(a**2))/((a+b)**2)
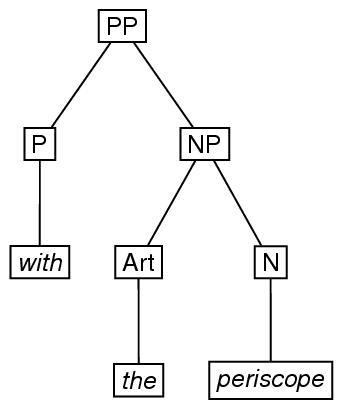
言語学でいう句構造は,一般に,木で表現される. 句構造を,例えば,一番上が根要素である,順序付きの根付き木で表 現すると,以下のようになる.
n="ex3"
ord="true"
arity="2"
order="8">
<root xml:id="GD-PP1" children="#GD-P1 #GD-NP1">
<label>PP</label>
</root>
<iNode xml:id="GD-P1" parent="#GD-PP1" children="#GD-WITH1">
<label>P</label>
</iNode>
<leaf xml:id="GD-WITH1" parent="#GD-P1">
<label>with</label>
</leaf>
<iNode xml:id="GD-NP1" parent="#GD-PP1" children="#GD-THE1 #GD-PERI1">
<label>NP</label>
</iNode>
<iNode xml:id="GD-ART1" parent="#GD-NP1" children="#GD-THE1">
<label>Art</label>
</iNode>
<leaf xml:id="GD-THE1" parent="#GD-ART1">
<label>the</label>
</leaf>
<iNode xml:id="GD-N1" parent="#GD-NP1" children="#GD-PERI1">
<label>N</label>
</iNode>
<leaf xml:id="GD-PERI1" parent="#GD-N1">
<label>periscope</label>
</leaf>
</tree>
また,順序付き木の例として,一般には他のノードよりも先行してある 特定のノードが,後で出現するようなものを考えてみる. 図上にある記号「xxx」は,VBからPTへの弧と,VPからPNへ の弧が,交差していることを示している(訳注:ノードではない.ガ イドラインでは,このようなものも木としている).
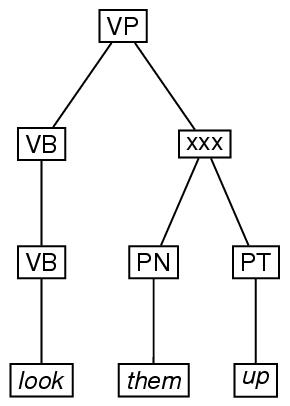
n="ex4"
arity="2"
order="8"
ord="true">
<leaf xml:id="GD-LOOK1" parent="#GD-VB2">
<label>look</label>
</leaf>
<leaf xml:id="GD-THEM1" parent="#GD-PN1">
<label>them</label>
</leaf>
<leaf xml:id="GD-UP1" parent="#GD-PT1">
<label>up</label>
</leaf>
<iNode xml:id="GD-VB2" parent="#GD-VB1" children="#GD-LOOK1">
<label>VB</label>
</iNode>
<iNode xml:id="GD-PN1" parent="#GD-VP1" children="#GD-THEM1">
<label>PN</label>
</iNode>
<iNode
xml:id="GD-PT1"
parent="#GD-VB1"
children="#GD-UP1"
follow="#GD-PN1">
<label>PT</label>
</iNode>
<iNode xml:id="GD-VB1" parent="#GD-VP1" children="#GD-VB2 #GD-PT1">
<label>VB</label>
</iNode>
<root xml:id="GD-VP1" children="#GD-VB1 #GD-PN1">
<label>VP</label>
</root>
</tree>
- « 19.2 木
- » 19.4 テキスト変遷の表示法
- Home | 目次
19.3 他の木表現TEI: 他の木表現¶
- eTree
順序付き根付き木を構成する部分木を示す.
value 当該部分木の値を示す.素性構造または他の分析に関する 要素になる. - triangle
未定義の部分木(eTree),すなわち情報が付与されていない部分
木を示す.
value 省略部分木の値を示す.素性構造または他の分析要素の識 別子になる. - eLeaf
部分木における葉を示す.要素eTree中で使用される.
value 部分木の葉の値を示す.この葉は,素性構造または他の分 析に関する要素である. - forest
根付き木の集合を示す.
type 当該森の種類を示す. - forestGrp
森の集合を示す.
type 当該森集合の種類を示す.
要素treeに ある 要素rootや 要素iNode や要素tree と同様に,要素eTreeや,要素triangle や,要素eLeafも,属性valueと要素labelを取ることが出来る.
要素eTree と要素eLeafの使い方を例示するため, 19.2 木で紹介した2番目の 例を再び使うと,以下のようになる.
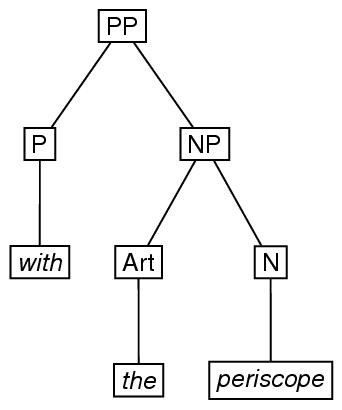
<label>PP</label>
<eTree>
<label>P</label>
<eLeaf>
<label>with</label>
</eLeaf>
</eTree>
<eTree>
<label>NP</label>
<eTree>
<label>Art</label>
<eLeaf>
<label>the</label>
</eLeaf>
</eTree>
<eTree>
<label>N</label>
<eLeaf>
<label>periscope</label>
</eLeaf>
</eTree>
</eTree>
</eTree>
次に,要素triangleの使い方を紹介する. この例では,ラベルNPを持つ要素eTreeの 内部構造は省略されている.
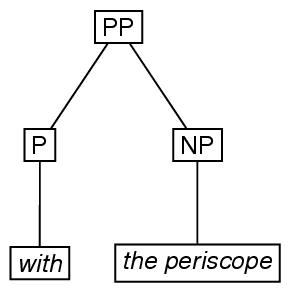
<label>PP</label>
<eTree>
<label>P</label>
<eLeaf>
<label>with</label>
</eLeaf>
</eTree>
<triangle>
<label>NP</label>
<eLeaf>
<label>the periscope</label>
</eLeaf>
</triangle>
</eTree>
同じ終端文字列を持つ複数の木構造の選択に伴う曖昧性は, 16.8 選択と 16.6 同一要素と仮想複製で解 説される属性excludeやcopyOfを使うことで,比較的容易に明示化す ることが出来る. 一番簡単な例としては,要素eTreeが,2つの異なる要素eTreeのうち,一 方の部分であるような場合である. これを符号化するには,埋め込まれている要素 eTreeに付 いての情報を,それを埋め込む(訳注:親要素となる)要素eTreeの中で 指定し,その内容のコピーを,属性copyOfで示すことになる. また,埋め込まれた要素が,他の要素と排他的な関係にある場合には, 属性excludeで示すことが出来る. 例えば,英語の表現「see the vessel with the periscope」を考えてみよう. この句は,構造上曖昧である. すなわち,「with the periscope(潜望鏡)」 は,「the vessel(船)」を修飾し ているのか(訳注:潜望鏡付き船),「see th evessel(船を覗く)」を修飾しているのか(訳注:潜望鏡で 船を覗く),曖昧である. 以下の図では,この曖昧さを,波線で示した弧で示している. 属性copyOfと属性exclude使うと,これは以下のように示すことが 出来る.
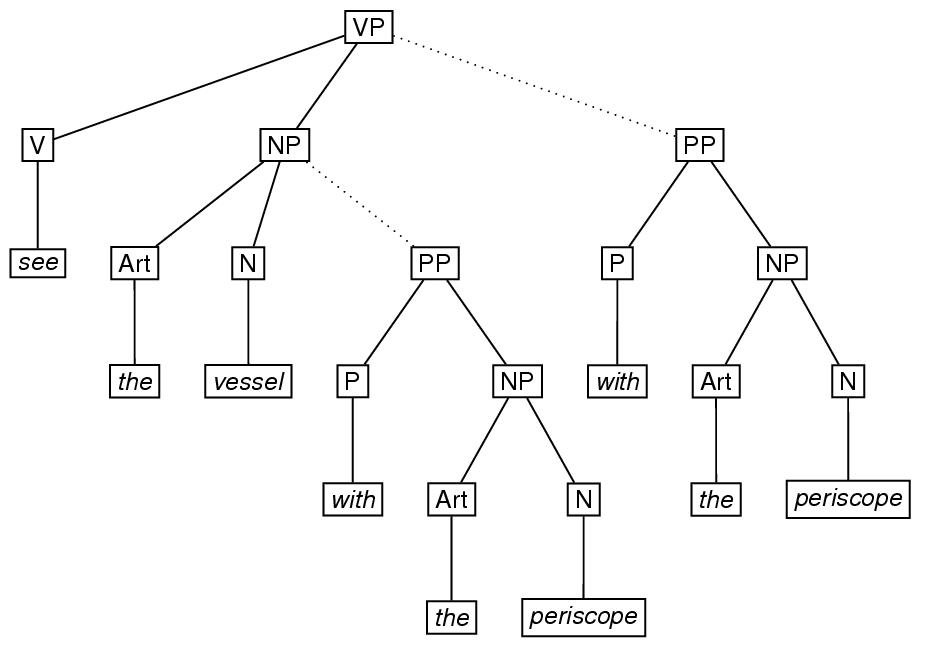
<label>VP</label>
<eTree>
<label>V</label>
<eLeaf>
<label>see</label>
</eLeaf>
</eTree>
<eTree>
<label>NP</label>
<eTree>
<label>Art</label>
<eLeaf>
<label>the</label>
</eLeaf>
</eTree>
<eTree>
<label>N</label>
<eLeaf>
<label>vessel</label>
</eLeaf>
</eTree>
<eTree xml:id="GD-PPA" exclude="#GD-PPB">
<label>PP</label>
<eTree>
<label>P</label>
<eLeaf>
<label>with</label>
</eLeaf>
</eTree>
<eTree>
<label>NP</label>
<eTree>
<label>Art</label>
<eLeaf>
<label>the</label>
</eLeaf>
</eTree>
<eTree>
<label>N</label>
<eLeaf>
<label>periscope</label>
</eLeaf>
</eTree>
</eTree>
</eTree>
</eTree>
<eTree xml:id="GD-PPB" copyOf="#GD-PPA" exclude="#GD-PPA">
<label>PP</label>
</eTree>
</eTree>
このような選択肢の中からひとつを選ぶ場合には,#GD-PPAまたは#GD-PPBのような,一番高階の要素eTreeに,属 性selectを付加して,示すことができ る. この詳細は,16.8 選択を参照のこと.
「see the man with the periscope(訳注:原文ママ)」のような例文の文法構造を表 現する場合,使用する文法によっては,先の例よりも,かなり複雑なものになるか もしれない. 例えば,ジャケンドフが主張した(訳注:生成文法でいう)Xバー理論 に従えば76,修飾句に は,実際に使われるときには現れない,中間ノードが存在する. これを図示すれば,以下のようになる. この図にある曖昧な構造を符号化すると,例えば,以下のようになる.
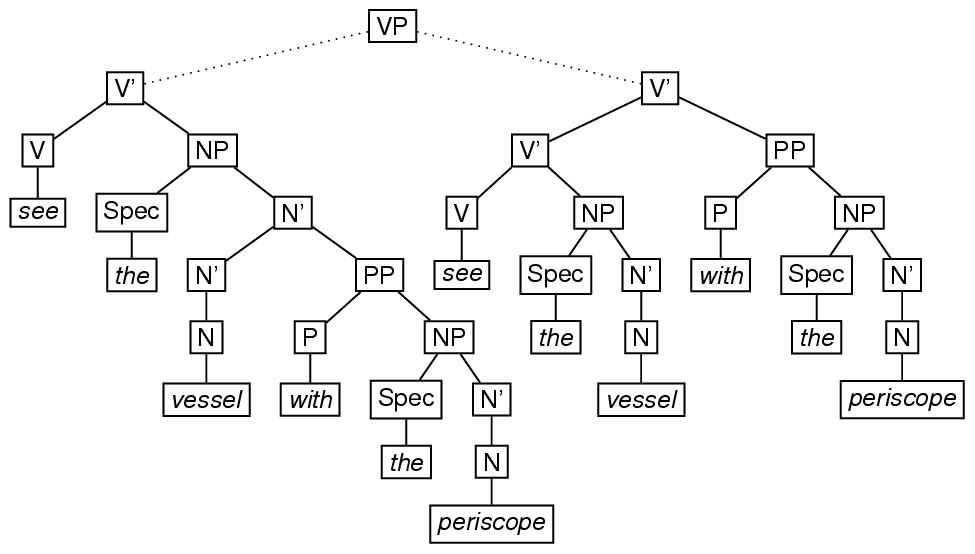
<label>VP</label>
<eTree xml:id="VBARA" exclude="#VBARB">
<label>V'</label>
<eTree xml:id="VA">
<label>V</label>
<eLeaf>
<label>see</label>
</eLeaf>
</eTree>
<eTree>
<label>NP</label>
<eTree xml:id="SPEC1A">
<label>Spec</label>
<eLeaf>
<label>the</label>
</eLeaf>
</eTree>
<eTree>
<label>N'</label>
<eTree xml:id="NBAR2A">
<label>N'</label>
<eTree>
<label>N</label>
<eLeaf>
<label>vessel</label>
</eLeaf>
</eTree>
</eTree>
<eTree xml:id="PPA1">
<label>PP</label>
<eTree>
<label>P</label>
<eLeaf>
<label>with</label>
</eLeaf>
</eTree>
<eTree>
<label>NP</label>
<eTree>
<label>Spec</label>
<eLeaf>
<label>the</label>
</eLeaf>
</eTree>
<eTree>
<label>N'</label>
<eTree>
<label>N</label>
<eLeaf>
<label>periscope</label>
</eLeaf>
</eTree>
</eTree>
</eTree>
</eTree>
</eTree>
</eTree>
</eTree>
<eTree xml:id="VBARB" exclude="#VBARA">
<label>V'</label>
<eTree>
<label>V'</label>
<eTree xml:id="VB" copyOf="#VA">
<label>V</label>
</eTree>
<eTree>
<label>NP</label>
<eTree xml:id="SPEC1B" copyOf="#SPEC1A">
<label>Spec</label>
</eTree>
<eTree xml:id="NBAR2B" copyOf="#NBAR2A">
<label>N'</label>
</eTree>
</eTree>
</eTree>
<eTree xml:id="PPB" copyOf="#PPA1">
<label>PP</label>
</eTree>
</eTree>
</eTree>
生成文法では,(訳注:文法から実際の文が生み出される工程である) 「導出」は,木の集合と解釈されることが多い. この導出を符号化するために,要素forestを使 うことができる. これにより,木を,要素treeや,要素eTreeや要素 triangleで示すことが出来る. 属性typeを使い,導出の種類を特定する ことも可能である. 例として,(例えば,this is what you doという文中にある)句「what you do」は,「you do what」 という句に,wh移動(wh-movement)が施されて,導出されているが, これは,2つの木から成る森で説明される. 77
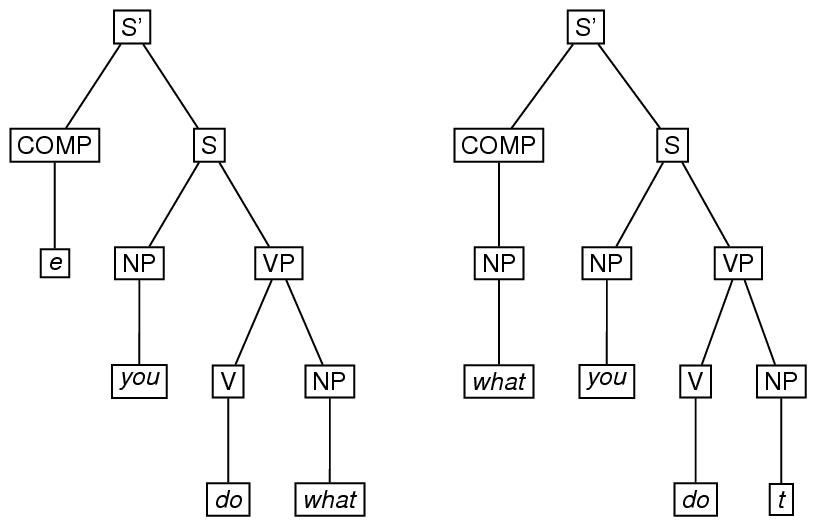
<eTree n="Stage 1" xml:id="S1SBAR">
<label>S'</label>
<eTree xml:id="S1COMP">
<label>COMP</label>
<eLeaf xml:id="S1E">
<label>e</label>
</eLeaf>
</eTree>
<eTree xml:id="S1S">
<label>S</label>
<eTree xml:id="S1NP1">
<label>NP</label>
<eLeaf>
<label>you</label>
</eLeaf>
</eTree>
<eTree xml:id="S1VP">
<label>VP</label>
<eTree xml:id="S1V">
<label>V</label>
<eLeaf>
<label>do</label>
</eLeaf>
</eTree>
<eTree xml:id="S1NP2">
<label>NP</label>
<eLeaf xml:id="S1WH">
<label>what</label>
</eLeaf>
</eTree>
</eTree>
</eTree>
</eTree>
<eTree n="Stage 2" xml:id="S2SBAR" corresp="#S1SBAR">
<label>S'</label>
<eTree xml:id="S2COMP" corresp="#S1COMP">
<label>COMP</label>
<eTree copyOf="#S1NP2" corresp="#S1E">
<label>NP</label>
</eTree>
</eTree>
<eTree xml:id="S2S" corresp="#s1s">
<label>S</label>
<eTree xml:id="S2NP1" copyOf="#S1NP1">
<label>NP</label>
</eTree>
<eTree xml:id="S2VP" corresp="#S1VP">
<label>VP</label>
<eTree xml:id="S2V" copyOf="#S1V">
<label>V</label>
</eTree>
<eTree xml:id="S2NP2" corresp="#S1NP2">
<label>NP</label>
<eLeaf corresp="#S1WH">
<label>t</label>
</eLeaf>
</eTree>
</eTree>
</eTree>
</eTree>
</forest>
この例では,属性copyOfを使い,1番目の 段階に出現している要素を,2番目の段階においては,そのコピーと して表現している. また,属性corresp(16.4 対応と統合)を使い,2番 目の段階にある,1番目の段階で出現している要素のコピーを,1番目 の段階に出現している要素からリンクにより関連づけている.
森の集合(例えば,構文的,意味的,音韻的な全ての導出を含むもの) を符号化したい時には,それらをまとめる要素forestGrpを使うことができる.
- « 19.3 他の木表現
- » 19.5 グラフモジュール
- Home | 目次
19.4 テキスト変遷の表示法TEI: テキスト変遷の表示法¶
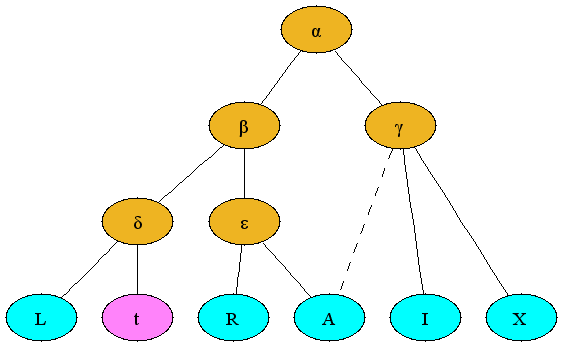
この系統樹にあるノードは,それぞれが写本を示している. ノードには,(1文字の)ラベルが振られており,これで写本を識別 し,また,それが現存しているか,現存していないか,想定上のもの かも示している. 現存する写本は,ラテン文字の大文字で表される. または,ラテン文字の大文字で始まる単語で表される. 例えば,上記の例では,Lがそれにあたる. その写本は,もやは現存していないが,その内容は,例えば,注釈書 や,その写本が失われる以前に伝えられたものから,その内容が 分かる場合,それは,ラテン文字の小文字で表される. 例えば,上記の例では,赤色のtがそれに あたる. テキストが伝わった上で想定されるもので,必ずしも現実にある写本 と対応している必要はないものは,ギリシャ文字の小文字で表される. 例えば,上記の例では,茶色のαがそれ にあたる. この系統図では(伝来の写本と失われた写本の類似性をもとに,Lとtにあるテキスト は,他の写本(例えば,δで示されたもの)に はないことが示されている. また,このテキストを証拠立てる実際の写本が見つけられていないこ とも示されている.
写本は,別の写本を底本としている. 先の系統図では,伝来の全ての写本は,ひとつの底本(α)から写し伝えられたものとしている. また,ある時代に,2つの系統(βとγ)に分かれたとしている. 伝わった写本が残っている場合は,その系統は実線で示されている. このモデルに従えば,αは,一番古い, 共通の,想定上可能なのものであり,α の子ノードは全てαを親としている. つまり,ひとつのものから,他のものは伝わっていることになる.
このような系統樹のモデルは,実際は,複雑で難しい. 理由は,写本は(訳注:ひとつの底本に寄らずに)複数のものからの影 響を受けていることがあるからである. 筆写者が,底本とは別の写本にある同じテキストを調べた結果作られ た可能性や,かつて読み知った元の本の記憶を頼りに修正した結果で ある可能性もある. または,筆写者Aが,ある底本を元にした写本を,筆写者Bが,その写 本にある余白や行間に(他の資料を直接調べたり自らの記憶を頼りに) 書き込みを加え,さらに別の者筆者が,その写本を底本にしながら, 本文に修正を加えた可能性もある. どのようなケースにせよ,写本がひとつの資料をもとに書き写されて 作られることは一般的ではなく,作られる写本は,伝来されていた多 くのものを統合したものである. このような複合的な成果物は「混合(contamination)」(訳注:「校定 本」にあたるもの)と呼ばれるもので,図上では,その関係が波線で 示されている. すると,この系統図では,Aはεを底本としながら,γ とも校合した結果を反映したものとなっている.
視覚化された系統図の便利さは,写本の伝来で発生する混合の程度 と,比例している. 混合が全くなく写本が伝わる(閉じた伝来(closed tradition))のであ れば,伝統的な木の形を作るので,系統図は簡単に図示することがで きる. 一方,混合が沢山あるような,閉じた伝来(open tradition)であれ ば,まるでスパゲティのように波線が絡み合った系統図が出来てしま い,これは読むのも困難で,役に立つものではない.
<label>δ</label>
<eLeaf type="extant">
<label>L</label>
</eLeaf>
<eLeaf type="lost">
<label>t</label>
</eLeaf>
</eTree>
<label>α</label>
<eTree type="hypothetical">
<label>β</label>
<eTree type="hypothetical">
<label>δ</label>
<eLeaf type="extant">
<label>L</label>
</eLeaf>
<eLeaf type="lost">
<label>t</label>
</eLeaf>
</eTree>
<eTree type="hypothetical">
<label>ε</label>
<eLeaf type="extant">
<label>R</label>
</eLeaf>
<eLeaf type="extant">
<label>A</label>
<ptr type="contamination" target="#gamma"/>
</eLeaf>
</eTree>
</eTree>
<eTree xml:id="gamma" type="hypothetical">
<label>γ</label>
<eLeaf type="extant">
<label>I</label>
</eLeaf>
<eLeaf type="extant">
<label>X</label>
</eLeaf>
</eTree>
</eTree>
実際の写本の研究では,このような簡単な構造ではなく,個々の実現 形に関するより詳細なデータが必要となるだろう. 本ガイドラインでは,この種の情報を記録するための,各種の要素を 用意している. これらの詳細は,10 Manuscript Description, 11 Representation of Primary Sources, 12 校本を参照のこと.
- « 19.4 テキスト変遷の表示法
- Home | 目次
